环己三烯的冬眠舱

天天网抑云，偶尔读点书。

0%

发表于

Tags

日期 2022年9月18日
是否独立完成 是
涉及算法 广度优先搜索、哈希表

题面

LeetCode 827. 最大人工岛

给你一个大小为 n x n 二进制矩阵 grid 。最多 只能将一格 0 变成 1 。

返回执行此操作后，grid 中最大的岛屿面积是多少？

岛屿 由一组上、下、左、右四个方向相连的 1 形成。

示例 1：

1
2
3
输入: grid = [[1, 0], [0, 1]]
输出: 3
解释: 将一格0变成1，最终连通两个小岛得到面积为 3 的岛屿。

示例 2：

1
2
3
输入: grid = [[1, 1], [1, 0]]
输出: 4
解释: 将一格0变成1，岛屿的面积扩大为 4。

示例 3：

1
2
3
输入: grid = [[1, 1], [1, 1]]
输出: 4
解释: 没有0可以让我们变成1，面积依然为 4。

题解

广度优先搜索+哈希表

可以用广度优先搜索把每个岛都标记成对应的下标（为了方便后续统计总面积，将下标定为由-1开始增长的负整数），每搜索完一个岛就把其对应的面积存在哈希表里。然后第开始第二次遍历，遇到0就计算其周围四格的岛的面积，并实时更新最大值。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution {
public:
    int largestIsland(vector<vector<int>>& grid) {
        int n = grid.size();
        unordered_map<int, int> area;
        int idx = -1;
        vector<int> dir{ -1,0,1,0,-1 };
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] != 1) continue;
                queue<pair<int, int>> q;
                q.push({ i,j });
                int cnt = 0;
                while (!q.empty()) {
                    pair<int, int> cur = q.front();
                    q.pop();
                    int r = cur.first, c = cur.second;
                    if (grid[r][c] < 0) continue;
                    grid[r][c] = idx;
                    for (int d = 0; d < 4; d++) {
                        int nr = r + dir[d], nc = c + dir[d + 1];
                        if (nr < 0 || nr >= n || nc < 0 || nc >= n || grid[nr][nc] <= 0) continue;
                        q.push({ nr,nc });
                    }
                    cnt++;
                }
                area[idx] = cnt;
                idx--;
            }
        }
        int res = -1;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] != 0) continue;
                unordered_set<int> visited;
                for (int d = 0; d < 4; d++) {
                    int ni = i + dir[d], nj = j + dir[d + 1];
                    if (ni < 0 || ni >= n || nj < 0 || nj >= n || grid[ni][nj] >= 0 || visited.count(grid[ni][nj])) continue;
                    visited.insert(grid[ni][nj]);
                    grid[i][j] += area[grid[ni][nj]];
                }
                res = max(res, grid[i][j]);
            }
        }
        if (res == -1) return area[-1];
        else return res + 1;
    }
};

发表于

Tags

日期 2022年9月17日
是否独立完成 否
涉及算法 动态规划 Again & Again

题面

LeetCode 940. 不同的子序列 II

给定一个字符串 s，计算 s 的 不同非空子序列 的个数。因为结果可能很大，所以返回答案需要对 10^9 + 7 取余 。

字符串的 子序列 是经由原字符串删除一些（也可能不删除）字符但不改变剩余字符相对位置的一个新字符串。

  • 例如，"ace" 是 "abcde" 的一个子序列，但 "aec" 不是。

示例 1：

1
2
3
输入：s = "abc"
输出：7
解释：7 个不同的子序列分别是 "a", "b", "c", "ab", "ac", "bc", 以及 "abc"。

示例 2：

1
2
3
输入：s = "aba"
输出：6
解释：6 个不同的子序列分别是 "a", "b", "ab", "ba", "aa" 以及 "aba"。

示例 3：

1
2
3
输入：s = "aaa"
输出：3
解释：3 个不同的子序列分别是 "a", "aa" 以及 "aaa"。

题解

动态规划

如果s中的字符是无重复的就很简单了，针对每个字符“取”或者“不取”都有两种可能，定义dp[i]为s前i个字母的不同非空子序列的个数，就可以引出转移公式dp[i+1]=dp[i]*2。

但是s中的字符是有重复的，所以要考虑去重的事。例如s="abb"，其中的a和两个b均能分别组成一次’ab’，所以要去掉一次，即dp[i+1]=dp[i]*2-dp[last]

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int distinctSubseqII(string s) {
        int mod = 1e9+7;
        int n = s.length();
        vector<int> dp(n+1);
        unordered_map<char,int> map;
        dp[0]=1;
        for(int i=0;i<n;i++){
            dp[i+1]=dp[i]*2 % mod;
            if(map.count(s[i])) dp[i+1]-=dp[map[s[i]]];
            dp[i+1]%=mod;
            map[s[i]]=i;
        }
        return (dp[n]-1+mod) % mod;
    }
};

发表于 更新于

Tags

日期 2022年9月15日
是否独立完成 否（差一点点！）
涉及算法 动态规划Again

题面

LeetCode 1771. 由子序列构造的最长回文串的长度

给你两个字符串 word1 和 word2 ，请你按下述方法构造一个字符串：

  • 从 word1 中选出某个 非空 子序列 subsequence1 。
  • 从 word2 中选出某个 非空 子序列 subsequence2 。
  • 连接两个子序列 subsequence1 + subsequence2 ，得到字符串。

返回可按上述方法构造的最长 回文串 的 长度 。如果无法构造回文串，返回 0 。

字符串 s 的一个 子序列 是通过从 s 中删除一些（也可能不删除）字符而不更改其余字符的顺序生成的字符串。

回文串 是正着读和反着读结果一致的字符串。

示例 1：

1
2
3
输入：word1 = "cacb", word2 = "cbba"
输出：5
解释：从 word1 中选出 "ab" ，从 word2 中选出 "cba" ，得到回文串 "abcba" 。

示例 2：

1
2
3
输入：word1 = "ab", word2 = "ab"
输出：3
解释：从 word1 中选出 "ab" ，从 word2 中选出 "a" ，得到回文串 "aba" 。

示例 3：

1
2
3
输入：word1 = "aa", word2 = "bb"
输出：0
解释：无法按题面所述方法构造回文串，所以返回 0 。

题解

动态规划

怎么Hard题这么多动态规划啊。而且与回文串有关的题题号也恰好是回文的，有点巧妙。

一开始的思路是把word2给reverse一下，然后通过动态规划算word1和word2的最长公共子序列，就可以得到答案了。但是遇到了下面这个测试用例WA了。

1
2
string word1 = "afaaadacb";
string word2 = "ca";

WA后初步认为是两个串不一样长导致的，所以添加了平衡字符串长度的代码，然后发现并不是长度的原因。还是得把两个串合在一起dp，并只在两个子串都不为空时更新答案。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    int longestPalindrome(string word1, string word2) {
        int n1 = word1.length(), n2 = word2.length();
        int n = n1 + n2;
        string word = word1 + word2;
        vector<vector<int>> dp(n, vector<int>(n, 0));
        int res = (word[n1 - 1] == word[n1]) ? 2 : 0;
        for (int i = 0; i < n; i++) dp[i][i] = 1;
        for (int i = 0; i < n - 1; i++) dp[i][i + 1] = (word[i] == word[i + 1]) ? 2 : 1;
        for (int l = 2; l < n; l++) {
            for (int i = 0; i + l < n; i++) {
                int j = i + l;
                if (word[i] == word[j]) {
                    dp[i][j] = dp[i + 1][j - 1] + 2;
                    if (i < n1 && j >= n1) res = max(res, dp[i][j]);
                }
                else dp[i][j] = max(dp[i][j - 1], dp[i + 1][j]);
            }
        }
        return res;
    }
};

有的没的

没事听点歌（Knock 2 - dashstar*）

发表于

Tags

日期 2022年9月14日
是否独立完成 否
涉及算法 暴力枚举、几何

题面

LeetCode 149. 直线上最多的点数

给你一个数组 points ，其中 points[i] = [xi, yi] 表示 X-Y 平面上的一个点。求最多有多少个点在同一条直线上。

示例 1：

1
2
输入：points = [[1,1],[2,2],[3,3]]
输出：3

示例 2：

1
2
输入：points = [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]]
输出：4

题解

暴力枚举

对于点a,b,c，如果其中任意两点构成的直线斜率相同，则三点共线。我们可以枚举所有的点对，用哈希表记录斜率，则可以判断有多少个点出现在同一条直线上。

本题难点在于计算斜率需要用到除法，而浮点数的除法是存在误差的。为了避免这个误差，一共有两种思路：

  1. 利用乘法来避免除法（把两个斜率相等的表达式用对角相乘法则化为两个乘法表达式相等）。
  2. 用字符串来哈希。

本题我选择用第二个思路解。在计算斜率时通过最大公约数把分式约分为最间，保证相同斜率的直线能全部哈希在一起。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
private:
    int gcd(int a, int b) {
        return b == 0 ? a : gcd(b, a % b);
    }
public:
    int maxPoints(vector<vector<int>>& points) {
        int res = 0;
        for (int i = 0; i < points.size(); i++) {
            unordered_map<string, int> map;
            int mx = 0;
            for (int j = i + 1; j < points.size(); j++) {
                int x1 = points[i][0], y1 = points[i][1];
                int x2 = points[j][0], y2 = points[j][1];
                int a = x1 - x2;
                int b = y1 - y2;
                int g = gcd(a, b);
                string key = to_string(a / g) + "_" + to_string(b / g);
                map[key]++;
                mx = max(mx, map[key]);
            }
            res = max(res, mx + 1);
        }
        return res;
    }
};

发表于 更新于

Tags

日期 2022年9月13日
是否独立完成 否
涉及算法 滑动窗口（或前缀和）、动态规划

题面

LeetCode 689. 三个无重叠子数组的最大和

给你一个整数数组 nums 和一个整数 k ，找出三个长度为 k 、互不重叠、且全部数字和（3 * k 项）最大的子数组，并返回这三个子数组。

以下标的数组形式返回结果，数组中的每一项分别指示每个子数组的起始位置（下标从 0 开始）。如果有多个结果，返回字典序最小的一个。

示例 1：

1
2
3
4
输入：nums = [1,2,1,2,6,7,5,1], k = 2
输出：[0,3,5]
解释：子数组 [1, 2], [2, 6], [7, 5] 对应的起始下标为 [0, 3, 5]。
也可以取 [2, 1], 但是结果 [1, 3, 5] 在字典序上更大。

示例 2：

1
2
输入：nums = [1,2,1,2,1,2,1,2,1], k = 2
输出：[0,2,4]

题解

滑动窗口 + 动态规划

看到多个子数组求和第一反应就是前缀和，后来看题解发现滑动窗口也可以，而且更省内存一点。

求完所有长度为k的子数组和后，可以维护一个left和一个right数组，其中left 存从左开始到当前位置最大的和，right存从右开始到当前位置最大的和。我们枚举处于中间位置的数组，再通过left和right快速检索与这个位置不冲突的左侧最大子数组和以及右侧最大子数组和，在枚举过程中不断更新结果就可以了。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    vector<int> maxSumOfThreeSubarrays(vector<int>& nums, int k) {
        vector<int> sum;
        int cur = 0;
        for (int i = 0; i < k; i++) cur += nums[i];
        sum.push_back(cur);
        int n = nums.size();
        for (int i = k; i < n; i++) {
            cur = cur + nums[i] - nums[i - k];
            sum.push_back(cur);
        }
        n = sum.size();
        vector<int> left(n, 0);
        vector<int> right(n, n - 1);
        for (int i = 1; i < n; i++) {
            if (sum[i] > sum[left[i - 1]]) left[i] = i;
            else left[i] = left[i - 1];
        }
        for (int i = n - 2; i >= 0; i--) {
            if (sum[i] >= sum[right[i + 1]]) right[i] = i;
            else right[i] = right[i + 1];
        }
        int mx = 0;
        vector<int> res(3, 0);
        for (int i = k; i < n - k; i++) {
            if (mx < sum[i] + sum[left[i - k]] + sum[right[i + k]]) {
                mx = sum[i] + sum[left[i - k]] + sum[right[i + k]];
                res = { left[i - k],i,right[i + k] };
            }
        }
        return res;
    }
};

有的没的

没事听点歌（One Republic - Counting Stars）

发表于

Tags

日期 2022年9月12日
是否独立完成 是
涉及算法 动态规划

题面

LeetCode 174. 地下城游戏

一些恶魔抓住了公主（P）并将她关在了地下城的右下角。地下城是由 M x N 个房间组成的二维网格。我们英勇的骑士（K）最初被安置在左上角的房间里，他必须穿过地下城并通过对抗恶魔来拯救公主。

骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下，他会立即死亡。

有些房间由恶魔守卫，因此骑士在进入这些房间时会失去健康点数（若房间里的值为负整数，则表示骑士将损失健康点数）；其他房间要么是空的（房间里的值为 0），要么包含增加骑士健康点数的魔法球（若房间里的值为正整数，则表示骑士将增加健康点数）。

为了尽快到达公主，骑士决定每次只向右或向下移动一步。

编写一个函数来计算确保骑士能够拯救到公主所需的最低初始健康点数。

例如，考虑到如下布局的地下城，如果骑士遵循最佳路径 右 -> 右 -> 下 -> 下，则骑士的初始健康点数至少为 7。

-2 (K) -3 3
-5 -10 1
10 30 -5 (P)

说明：

  • 骑士的健康点数没有上限。
  • 任何房间都可能对骑士的健康点数造成威胁，也可能增加骑士的健康点数，包括骑士进入的左上角房间以及公主被监禁的右下角房间。

题解

动态规划

随机刷居然能刷到做过的题，我还想这题还能是Hard…

动态规划经典题，从右下角向左上角dp，每个单元格表示在能救到公主的前提下进入该单元格前所需的最低生命值。最后dp[0][0] - dungeon[0][0]就是最终答案（当然，小于等于0当1处理）。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    int calculateMinimumHP(vector<vector<int>>& dungeon) {
        int m = dungeon.size();
        int n = dungeon[0].size();
        vector<vector<int>> dp(m, vector<int>(n, 0));
        dp[m - 1][n - 1] = 1;
        for (int i = m - 2; i >= 0; i--) {
            dp[i][n - 1] = dp[i + 1][n - 1] - dungeon[i + 1][n - 1];
            if (dp[i][n - 1] <= 0) dp[i][n - 1] = 1;
        }
        for (int i = n - 2; i >= 0; i--) {
            dp[m - 1][i] = dp[m - 1][i + 1] - dungeon[m - 1][i + 1];
            if (dp[m - 1][i] <= 0) dp[m - 1][i] = 1;
        }
        for (int i = m - 2; i >= 0; i--) {
            for (int j = n - 2; j >= 0; j--) {
                int a = dp[i][j + 1] - dungeon[i][j + 1];
                int b = dp[i + 1][j] - dungeon[i + 1][j];
                dp[i][j] = min(a, b);
                if (dp[i][j] <= 0) dp[i][j] = 1;
            }
        }
        int res = dp[0][0] - dungeon[0][0];
        return  res <= 0 ? 1 : res;
    }
};

有的没的

关于每日Hard

题已经刷了不少了，接下来打算加大刷题的难度。其实暑假期间就计划要每日一题Hard来着，后来没坚持几天就摸了。于是决定每次做完题来Blog打个卡，算是督促自己坚持刷题吧。也不是真的要每天做一题Hard，只能说在时间允许的前提下努力坚持吧。

发表于 更新于

概述

听名字就能大概猜出“有限状态自动机”是干嘛的了。

  • 有一个当前状态 pre

  • 每轮循环输入一个 cur

  • 有限状态自动机可以根据事先的定义来进行状态的转移

有限状态自动机并不能降低算法的复杂度，但是可以让代码看起来非常简洁清爽，也不会写着写着就晕掉了。

例题

剑指 Offer 20. 表示数值的字符串

请实现一个函数用来判断字符串是否表示数值（包括整数和小数）。

数值（按顺序）可以分成以下几个部分：

  1. 若干空格

  2. 一个 小数 或者 整数

  3. （可选）一个 'e' 或 'E' ，后面跟着一个 整数

  4. 若干空格

小数（按顺序）可以分成以下几个部分：

  1. （可选）一个符号字符（'+' 或 '-'）

  2. 下述格式之一：

    1. 至少一位数字，后面跟着一个点 '.'

    2. 至少一位数字，后面跟着一个点 '.'，后面再跟着至少一位数字

    3. 一个点 '.' ，后面跟着至少一位数字

整数（按顺序）可以分成以下几个部分：

  1. （可选）一个符号字符（’+’ 或 ‘-‘）

  2. 至少一位数字

部分数值列举如下：

  • ["+100", "5e2", "-123", "3.1416", "-1E-16", "0123"]

部分非数值列举如下：

  • ["12e", "1a3.14", "1.2.3", "+-5", "12e+5.4"]

示例 1：

1
2
输入：s = "0"
输出：true

示例 2：

1
2
输入：s = "e"
输出：false

示例 3：

1
2
输入：s = "."
输出：false

示例 4：

1
2
输入：s = "    .1  "
输出：true

题解

先贴一段我第一次写时的代码，用的是暴力模拟，写半天自己都写晕了，到后面变量名字都开始乱七八糟了，因为不能一次性考虑到所有细节， 所以根据WA给的测试用例缝缝补补勉强通过。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
private:
    stringstream ss;
public:
    bool isNumber(string s) {
        ss << s;
        ss >> ws;
        if(ss.peek()=='+' || ss.peek()=='-') ss.get();
        bool hasnum=false;
        while(isdigit(ss.peek())){
            ss.get();
            hasnum=true;
        }
        if(ss.peek()=='.') {
            ss.get();
            bool hasnum2=false;
            while(isdigit(ss.peek())){
                ss.get();
                hasnum2=true;
            }
            if(!hasnum2 && !hasnum) return false;
        }
        else if(!hasnum) return false;

        if(ss.peek()=='e' || ss.peek()=='E'){
            ss.get();
            bool hasnum1=false;
            if(ss.peek()=='+' || ss.peek()=='-') ss.get();
            while(isdigit(ss.peek())){
                ss.get();
                hasnum1=true;
            }
            if(!hasnum1) return false;
        }
        ss >> ws;
        return ss.peek()==-1;
        
    }
};

而使用有限状态自动机就可以让代码非常清晰。我们可以定义如下的状态：

图源：LeetCode @Krahets 前辈的题解

在代码中，我们使用数组+字典来储存上图。只有退出后的状态为 2/3/7/8 中的一个时，我们才认为输入的字符串为合法的数值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    bool isNumber(string s) {
        stringstream ss;
        ss << s;
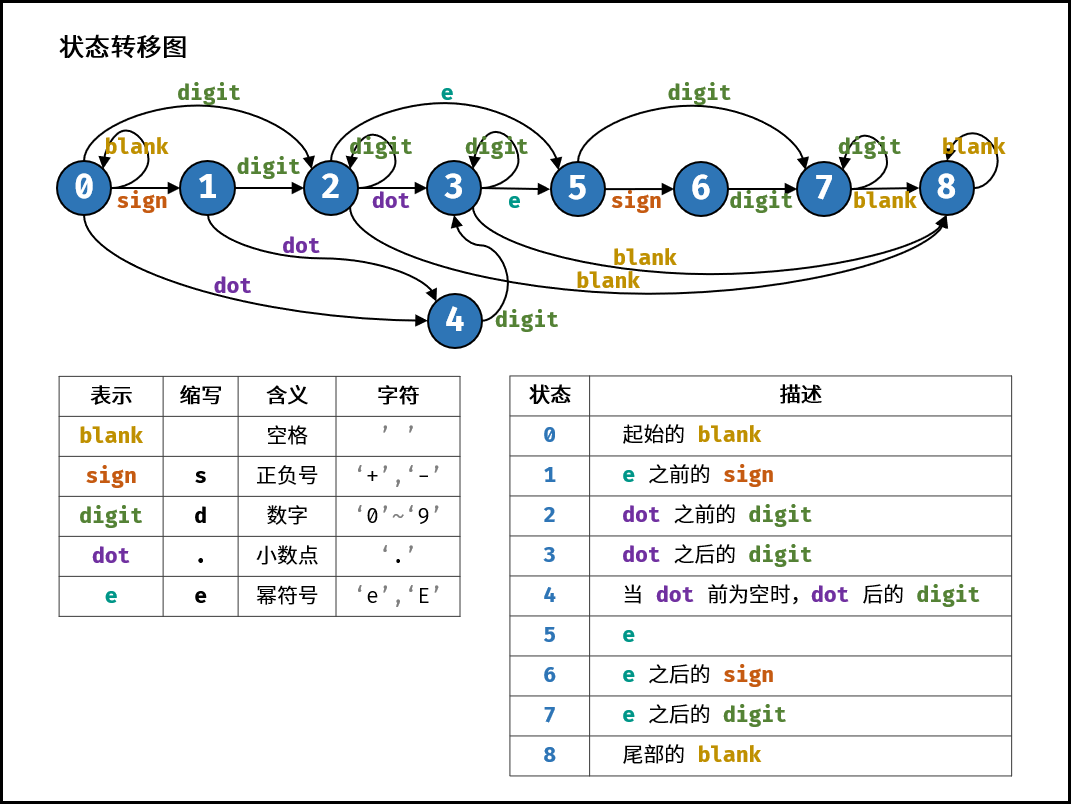
        vector<unordered_map<char, int>> states = {
            { {' ', 0},{ 's', 1},{ 'd', 2}, {'.', 4} },
            { {'d', 2},{ '.', 4} } ,
            { {'d', 2},{ '.', 3}, {'e', 5}, {' ', 8} },
            { {'d', 3}, {'e', 5}, {' ', 8} },
            { {'d', 3} },
            { {'s', 6}, {'d', 7} },
            { {'d', 7} },
            { {'d', 7}, {' ', 8} },
            { {' ', 8} }
        };
        int pre = 0;
        while (ss.peek() != -1) {
            char c = ss.get();
            char cur;
            if ('0' <= c && c <= '9') cur = 'd';
            else if (c == '+' || c == '-') cur = 's';
            else if (c == 'e' || c == 'E') cur = 'e';
            else if (c == '.' || c == ' ') cur = c;
            else cur = '?';
            if (states[pre].count(cur) <= 0) return false;
            pre = states[pre][cur];
        }
        return pre == 2 || pre == 3 || pre == 7 || pre == 8;
    }
};

有的没的

天才操作

13号回的学校。回校前精心挑选了一班快十几分钟的车次，然后当天到了宁波站了才发现终点站是杭州南，不是杭州东，少坐一站可不是快一点嘛。后来找乘务姐姐补了一站路。

新生要来报到了

明天新生就陆续要来报到了，我也该读大三了。没有人永远年轻，但永远有人年轻。

没事听点歌（Neck Deep - Serpent）

发表于 更新于

概述

今天LeetCode的每日一题是设计一个跳表。跳表是一种类似链表的数据结构，可以实现时间复杂度为 O(log n) 的查找和插入，效率堪比红黑树。

常规的链表可以实现常数级时间复杂度的插入，但是查找某一个特定元素的元素却是线性的。而诸如数组和vector之类的简单线性的数据结构，虽然可以通过二分查找来实现 O(log n) 时间复杂度的查找，但是在某个特定位置插入一个元素需要把其后面所有元素都挪动一遍，牵一发而动全身。而AVL树、红黑树可以平衡插入和查找的效率，被广泛应用。今天刚学到的跳表也有相似的性质。

插一个小故事。就前两天我在看《STL源码剖析》试图理解红黑树的时候还看到一段话，说普通的链表查找某一个特定元素是线性的，我就想这个作者也太菜了，你不能二分查找吗？后来仔细一想，才想起来原来链表是没法随机访问的，自然不能二分查找，是我太菜了。

后来还是看不懂红黑树是什么原理。但是跳表就好理解多了。在LeetCode评论区里看到一条，“想了半天要如何确定一个值应该占用几层的链表，然后你给我来个coin filp，我遭不住了，底层逻辑基于随机数，怪不得STL里没你”，笑死我了。

扯了这么多，那么跳表到底是什么原理呢？用LeetCode上的一张图就可以看懂了。

查找

查找时从上往下依次找到每层小于目标值的最大的节点，然后依次往下查找，中间可以跳过很多个节点。因为可以有可以跳过节点这个性质，跳表查找的平均时间复杂度是O(log n) ，这个有大佬证明了，而我不是大佬所以我不会证明。

插入

插入时也依次从上往下找插入的节点，第0层包含跳表内的所有元素，然后每个元素在插入时有p的概率可以加入到上面那层，p 一般被设置为 1/2 。没错，跳表的结构是随机出来的，就是这么草率。

例题

LeetCode 1206. 设计跳表

就是设计一个上述跳表，要求实现查找、插入和删除三个功能。

示例 1：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
输入
["Skiplist", "add", "add", "add", "search", "add", "search", "erase", "erase", "search"]
[[], [1], [2], [3], [0], [4], [1], [0], [1], [1]]
输出
[null, null, null, null, false, null, true, false, true, false]

解释
Skiplist skiplist = new Skiplist();
skiplist.add(1);
skiplist.add(2);
skiplist.add(3);
skiplist.search(0);   // 返回 false
skiplist.add(4);
skiplist.search(1);   // 返回 true
skiplist.erase(0);    // 返回 false，0 不在跳表中
skiplist.erase(1);    // 返回 true
skiplist.search(1);   // 返回 false，1 已被擦除

题解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
class Skiplist {
private:
    class Node {
    //链表的节点类，把插入和删除的操作都集成进来了
    public:
        int val;
        vector<Node* > next = vector<Node* >(10, nullptr);//为了偷懒这里直接把十层链表的头尾节点都预留好了，内存击败百分五[ac01]
        Node(int v) :val(v) {};//构造函数
        void insert(Node* nxt, int level) {
            //在当前节点后面插入节点nxt，level代表目前操作的层数
            vector<Node* >& cur = this->next;
            nxt->next[level] = cur[level];
            cur[level] = nxt;
            return;
        }
        void erasenext(Node* nxt) {
            //在整个跳表中移除节点nxt
            vector<Node* >& cur = this->next;
            for (int i = 0; i < 10; i++) {
                if (cur[i] == nxt) {
                    cur[i] = cur[i]->next[i];
                }
            }
        }
    };
    //head和tail为头尾节点
    Node* head;
    Node* tail;
public:
    Skiplist() {
        //Skiplist类的构造函数，将head和tail进行初始化
        head = new Node(-1);
        tail = new Node(1e9 + 7);
        for (int i = 0; i < 10; i++) {
            //初始状态head的十个指针均应指向tail
            head->next[i] = tail;
        }
    }

    bool search(int target) {
        Node* cur = head;
        //从上往下依次找到每层比target小的最大节点
        for (int i = 9; i >= 0; i--) {
            while (cur->next[i]->val < target) cur = cur->next[i];
        }
        //如果最后一层的下一个节点的值不是target的话，那target一定不在跳表里。
        return cur->next[0]->val == target;
    }

    void add(int num) {
        /*前半部分和search过程一样
        只是需要多用一个stack把路上遇到的节点都存起来 */
        stack<Node* > stk;
        Node* cur = head;
        for (int i = 9; i >= 0; i--) {
            while (cur->next[i]->val < num) cur = cur->next[i];
            stk.push(cur);
        }
        int level = 0;
        Node* newnode = new Node(num);//创建新节点
        cur->insert(newnode, level);//第0层含有跳表全部元素，所以必须加入
        while (level < 9 && rand() % 2 == 0) {
            //进行一次判定，有1/2的几率可以进入上一层
            level++;
            stk.pop();
            stk.top()->insert(newnode, level);
        }
    }

    bool erase(int num) {
        //前半部分和add一样需要把路过的节点存起来
        stack<Node* > stk;
        Node* cur = head;
        for (int i = 9; i >= 0; i--) {
            while (cur->next[i]->val < num) cur = cur->next[i];
            stk.push(cur);
        }
        if (cur->next[0]->val != num) return false;//如果跳表里没有num就直接返回false
        else {
            /*否则调用erase函数删除后面一个节点
            此处传入的是节点的指针，保证不会误伤别的具有相同值的节点 */
            cur->erasenext(cur->next[0]);
            return true;
        }
    }
};

有的没的

暑假生活

暑假在家真的宅烂了，今天跟两个初中同学去南虹吃了一整天。吃了臭豆腐、老长沙手工肠、颜记排骨、虾滑、两杯茶百道、KFC、炸串串，饱死了。

没事听点歌（胡歌 - 忘记时间）

发表于 更新于

概述

并查集是用来处理一些不相交集合的合并和查询问题，开始时每个元素都是一个集合，然后在处理中会依据一些规则来进行集合的合并。在逻辑上，并查集是由很多树组成的森林，而在实际的代码中，我们往往使用数组来储存，数组的下标表示树的节点，下标对应的元素表示该节点的父节点。另外，我们定义根节点的父节点是它自己。并查集的操作有：

  • 查询某个节点的根节点

  • 合并两个集合

代码实现

初始化

首先定义一个 vector 来表示并查集。在初始化时，我们将其中每个元素设为其对应下标的值。

1
2
3
4
vector<int> vec;
//初始化代码
vec.resize(n, 0);//n代表元素的数量
for (int i = 0; i < n; i++) vec[i] = i;

查询

查询指查询给定节点的根节点。若两个节点的根节点相同，则表示这两个节点在同一个集合里。在代码中，如果某个节点不是根节点（表现为元素与其对应的下标不相等），则递归地查找其父节点的根节点，并将其父节点直接修改为根节点以减少下次查找所需要的时间（称为“路径压缩”）。

1
2
3
4
int find(int root) {
    if (vec[root] != root) vec[root] = find(vec[root]);
    return vec[root];
}

合并

合并指将给定两个节点所在的集合合并为一个集合。在代码中通过将其中一个集合的根节点的父节点设置成另一个节点的根节点，这样两个集合就有了共同的根节点，即合并为同一个集合了。

1
2
3
4
void union_root(int r1, int r2) {
    vec[find(r1)] = vec[find(r2)];
    return;
}

例题

LeetCode 765. 情侣牵手

n 对情侣坐在连续排列的 2n 个座位上，想要牵到对方的手。

人和座位由一个整数数组 row 表示，其中 row[i] 是坐在第 i 个座位上的人的 ID。情侣们按顺序编号，第一对是 (0, 1)，第二对是 (2, 3)，以此类推，最后一对是 (2n-2, 2n-1)。

返回 最少交换座位的次数，以便每对情侣可以并肩坐在一起。 每次交换可选择任意两人，让他们站起来交换座位。

示例 1：

1
2
3
输入: row = [0,2,1,3]
输出: 1
解释: 只需要交换row[1]和row[2]的位置即可。

示例 2:

1
2
3
输入: row = [3,2,0,1]
输出: 0
解释: 无需交换座位，所有的情侣都已经可以手牵手了。

题解

通过观察我们可以发现：

  • 如果有 2 对情侣彼此坐错了位置，则需要进行 1 次交换。

  • 如果有 3 对情侣彼此坐错了位置，则需要进行 2 次交换。

  • 如果有 4 对情侣彼此坐错了位置，则需要进行 3 次交换。

  • 如果有 n 对情侣彼此坐错了位置，则需要进行 n-1 次交换。

那么我们可以采用并查集的数据结构，将彼此坐错的情侣放进同一个集合，记并查集森林中有 cnt 棵树，共有 n 对情侣，那么需要交换的次数就是 n-cnt 。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
private:
    vector<int> vec;
    int find(int root) {
        if (vec[root] != root) vec[root] = find(vec[root]);
        return vec[root];
    }
    void union_root(int r1, int r2) {
        vec[find(r1)] = vec[find(r2)];
        return;
    }
public:
    int minSwapsCouples(vector<int>& row) {
        int n = row.size(); int m = n / 2;
        vec.resize(m, 0);
        for (int i = 0; i < m; i++) vec[i] = i;
        for (int i = 1; i <= m; i++) {
            union_root(row[2 * i - 2] / 2, row[2 * i - 1] / 2);
        }
        int cnt = 0;
        for (int i = 0; i < m; i++) {
            if (find(i) == i) cnt++;
        }
        return m - cnt;
    }
};

在代码中，我们用某个人的 ID 除以 2 来表示ta和ta对象共同的 情侣ID，然后把实际上挨着坐的人都 union 起来。如果他们本来就是情侣，则最终他们所在集合就只会有一个元素，表示这个集合中的人不需要交换。 union 到最后，我们得到的并查集中每个集合的情侣都坐混了，需要互相发生交换；而不同集合中的情侣之间则不需要发生交换。

有的没的

速通《空洞骑士》

这游戏很简单的，两个多小时就通关了(狗头)。

没事听点歌（莫文蔚 - 这世界那么多人）