好久不见,刚好一个月没更新了。一个月里还发生了蛮多事的,单一个防疫政策就已经大变天了。希望能看到这句话的朋友们都能保护好自己,能晚不早,能阴不阳。
概述
在线 和 离线 可以简单地理解为对于所有的操作是否需要读入完毕。
在线算法的要求是,不用先知道所有的操作(如查询、修改等),一边读入一边执行,所有操作之间的独立性比较高。
而离线算法则相反,要求必须先知道所有的操作,再执行操作。这样的话,我们就有机会合理安排操作顺序,以更高的效率完成所有操作。
例题
LeetCode 1697. 检查边长度限制的路径是否存在
给你一个 n 个点组成的无向图边集 edgeList ,其中 edgeList[i] = [ui, vi, disi] 表示点 ui 和点 vi 之间有一条长度为 disi 的边。请注意,两个点之间可能有 超过一条边 。
给你一个查询数组 queries ,其中 queries[j] = [pj, qj, limitj] ,你的任务是对于每个查询 queries[j] ,判断是否存在从 pj 到 qj 的路径,且这条路径上的每一条边都 严格小于 limitj 。
请你返回一个 布尔数组 answer ,其中 answer.length == queries.length ,当 queries[j] 的查询结果为 true 时, answer 第 j 个值为 true ,否则为 false 。
示例 1:
1
2
3
4
5
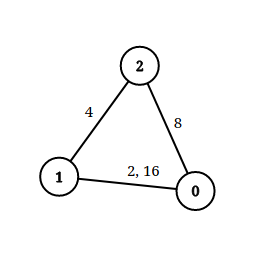
| 输入:n = 3, edgeList = [[0,1,2],[1,2,4],[2,0,8],[1,0,16]], queries = [[0,1,2],[0,2,5]]
输出:[false,true]
解释:上图为给定的输入数据。注意到 0 和 1 之间有两条重边,分别为 2 和 16 。
对于第一个查询,0 和 1 之间没有小于 2 的边,所以我们返回 false 。
对于第二个查询,有一条路径(0 -> 1 -> 2)两条边都小于 5 ,所以这个查询我们返回 true 。
|
示例 2:
1
2
3
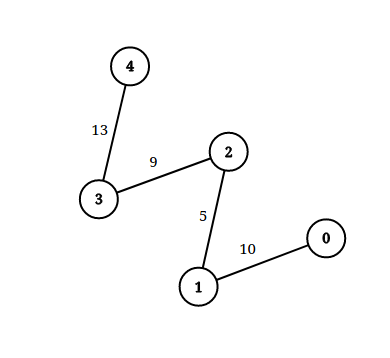
| 输入:n = 5, edgeList = [[0,1,10],[1,2,5],[2,3,9],[3,4,13]], queries = [[0,4,14],[1,4,13]]
输出:[true,false]
解释:上图为给定数据。
|
题解
我的第一反应是在线查询的思路,就是把每个 query 都当成独立的,然后再写一个函数判断是否可行,而这个函数的算法可能会采用BFS。后来觉得容易TLE,瞄了眼题解发现要用并查集。然后我就闷头写了个并查集,查询时,将边长度小于当前 query 限制距离的边的两个端点 union 起来,发现还是TLE。(有关并查集的内容可以查阅 这篇文章 。)
然后仔细研究了题解,发现了离线查询这东西。因为题目的查询操作都是给定的,所以我们可以根据每个 query的距离限制对 queries 数组进行升序排序,同时也根据边的长度对 edgeList 进行升序排序,再按照新的queries 顺序进行操作。这样,限制距离更小的 query 操作起来就是限制距离更大的 query 的子集,跟在线查询比都不知道省到哪里去了。
代码
C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| class Solution {
private:
vector<int> vec;
int find(int a) {
if (vec[a] == a) return a;
else {
int root = find(vec[a]);
vec[a] = root;
return root;
}
}
void uni(int a, int b) {
vec[find(a)] = find(b);
}
public:
vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edgeList, vector<vector<int>>& queries) {
vec = vector<int>(n, 0);
iota(vec.begin(), vec.end(), 0);
vector<bool> res(queries.size(), false);
sort(edgeList.begin(), edgeList.end(), [](vector<int>& e1, vector<int>& e2) {
return e1[2] < e2[2];
});
vector<int> seq(queries.size());
iota(seq.begin(), seq.end(), 0);
sort(seq.begin(), seq.end(), [&queries](int i1, int i2) {
return queries[i1][2] < queries[i2][2];
});
int idx = 0;
for (int i : seq) {
while (idx < edgeList.size() && edgeList[idx][2] < queries[i][2]) {
uni(edgeList[idx][0], edgeList[idx][1]);
idx++;
}
res[i] = (find(queries[i][0]) == find(queries[i][1]));
}
return res;
}
};
|
Go
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| func distanceLimitedPathsExist(n int, edgeList [][]int, queries [][]int) []bool {
vec := make([]int,n)
for i := range vec {
vec[i] = i
}
var find func(int) int
find = func(a int) int {
if vec[a] != a {
vec[a] = find(vec[a])
}
return vec[a]
}
union := func(a,b int) {
vec[find(a)] = find(b)
}
for i := range queries {
queries[i] = append(queries[i], i)
}
sort.Slice(edgeList,func(i,j int) bool {
return edgeList[i][2] < edgeList[j][2]
})
sort.Slice(queries,func(i,j int) bool {
return queries[i][2] < queries[j][2]
})
res := make([]bool,len(queries))
var idx int = 0
for _,query := range queries {
for idx < len(edgeList) && edgeList[idx][2] < query[2] {
union(edgeList[idx][0],edgeList[idx][1])
idx++
}
res[query[3]] = find(query[0]) == find(query[1])
}
return res
}
|
有的没的
入坑Golang
投实习的时候发现好多后端都要求用Go开发,于是决定入坑。语法上过了一遍菜鸟教程,然后力扣上题也刷起来了,中等以下的题都是直接用Go写,今天的Hard用C++写了一遍之后再用Go写了一遍。Go的语法就像是C/C++和Python的融合怪,取了二者之精华,还增加了一些C/C++并没有但是很实用很酷炫的特性(比如for … range语法可以同时迭代下标和值),我很中意。但也有很多有些别扭的地方,比如不支持set ,只有 map ,虽然本质上差不多,也可以用 map 实现 set 的功能,但是用起来就是很麻烦。还没内置 queue 、 stack 之类的数据结构,甚至连 min 、 max 这种简单而又常用的函数都需要自己手搓。STL真是绝绝子好用到跺jiojio。
没事听点歌(Coldplay - Viva La Vida)

