概述

线段树是树状数组的进阶版。说是进阶版，其实效率并没有提高，只是泛用性更广。线段树支持高效的单点查询、单点修改、区间查询、区间修改，但是代码比树状数组更复杂，所以只有迫不得已的时候才写线段树。

线段树就是一层一层地将原数据相加合并，最后形成一棵树的数据结构。用语言可能难以描述，但是看图就懂了：

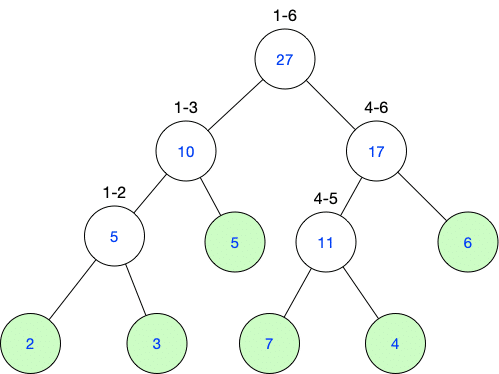
如此组织数据，就可以将区间查询的时间复杂度降低到 O(log n) ，而单点查询、单点修改的时间复杂度也被限制在可以接受的 O(log n) ，所以在数据量很大时可以有理想的效果。

做题时发现的一个缺点：由于要存储所以数据加起来的和，所以在数据较大时可能溢出。

代码实现

准备工作

由于线段树是类似完美二叉树的形式，所以我们可以使用数组来存储整棵树。对于某个下标为 root 的节点，它的左孩子节点下标为 root*2 ，右孩子节点下边为 root*2+1 。由于我们需要在原数组的基础上多储存若干个节点的和，所以线段树需要使用数倍于原数组的空间。一般上来说，我们在初始化线段树时，预留 3 ~ 4 倍于原数组的储存空间。

1	vector<int> tree(n*4,0);

构建线段树

void buildtree(int root, int start, int end){
    if(start == end){
        tree[root] = num[start];
        return;
    }
    int leftroot = root * 2;
    int rightroot = root * 2 + 1;
    int mid = (start + end) / 2;
    //递归地创建左右子树
    buildtree(leftroot,start,mid);
    buildtree(rightroot,mid+1,end);
    //左右子树创建完毕，根据左右子树根节点的值给当前的根赋值
    tree[root] = tree[leftroot] + tree[rightroot];
}

查询

int query(int root, int start, int end, int l, int r){
    //查询[l,r]区间的和。当l==r时即为单点查询。
    if(l <= start && r >= end) return tree[root];
    int leftroot = root * 2;
    int rightroot = root * 2 + 1;
    int mid = (start + end) / 2;
    int sum = 0;
    if(l <= mid) sum += query(leftroot,start,mid,l,r);
    if(r > mid) sum += query(rightroot,mid+1,end,l,r);
    return sum;
}

修改（低配版）

void update(int root, int start, int end, int l, int r, int k){
    //将区间[l,r]内全部元素加上k。当l==r时即为单点修改。
    if(start == end){
        tree[root] += k;
        return;
    }
    int leftroot = root * 2;
    int rightroot = root * 2 + 1;
    int mid = (start + end) / 2;
    if(l <= mid) update(leftroot,start,mid,l,r,k);
    if(r > mid) update(rightroot,mid+1,end,l,r,k);
    tree[root] = tree[leftroot] + tree[rightroot];
    return;
}

例题

LeetCode 1109. 航班预订统计

这里有 n 个航班，它们分别从 1 到 n 进行编号。

有一份航班预订表 bookings ，表中第 i 条预订记录 bookings[i] = [firstᵢ, lastᵢ, seatsᵢ] 意味着在从 firstᵢ 到 lastᵢ （包含 firstᵢ 和 lastᵢ ）的 每个航班 上预订了 seatsᵢ 个座位。

请你返回一个长度为 n 的数组 answer，里面的元素是每个航班预定的座位总数。

示例 1:

输入：bookings = [[1,2,10],[2,3,20],[2,5,25]], n = 5
输出：[10,55,45,25,25]
解释：
航班编号        1   2   3   4   5
预订记录 1 ：   10  10
预订记录 2 ：       20  20
预订记录 3 ：       25  25  25  25
总座位数：      10  55  45  25  25
因此，answer = [10,55,45,25,25]

示例 2：

输入：bookings = [[1,2,10],[2,2,15]], n = 2
输出：[10,25]
解释：
航班编号        1   2
预订记录 1 ：   10  10
预订记录 2 ：       15
总座位数：      10  25
因此，answer = [10,25]

题解

本题最合适的解法是差分数组（区间修改、单点查询）。但是也可以用线段树（虽然有些杀鸡用牛刀）。

注意：真正使用线段树的方法解出本题还需要线段树的进阶写法（Lazy Tag，懒标记），我将会在《线段树（下）》中介绍 ~~（如果你还看不到这篇文章，说明我还没写）~~。以下提供的代码只可以通过约三分之二的测试用例，剩余会超时，原因是目前使用的区间修改方法时间复杂度很高（如果没算错的话，应该是 O(nlog n) ，还没真正达到 O(log n) 的级别。

class Solution {
private:
    vector<long long> tree;
    int query(int root, int start, int end, int l, int r){
        if(l<=start && r>=end) return tree[root];
        int leftroot=root*2;
        int rightroot=root*2+1;
        int mid=(start+end)/2;
        int sum=0;
        if(l<=mid) sum+=query(leftroot,start,mid,l,r);
        if(r>mid) sum+=query(rightroot,mid+1,end,l,r);
        return sum;
    }
    void update(int root, int start, int end, int l, int r, int k){
        if(start==end){
            tree[root]+=k;
            return;
        }
        int leftroot=root*2;
        int rightroot=root*2+1;
        int mid=(start+end)/2;
        if(l<=mid) update(leftroot,start,mid,l,r,k);
        if(r>mid) update(rightroot,mid+1,end,l,r,k);
        tree[root]=tree[leftroot]+tree[rightroot];
        return;
    }
public:
    vector<int> corpFlightBookings(vector<vector<int>>& bookings, int n) {
        tree.resize(4*n,0);
        for(int i=0;i<bookings.size();i++){
            update(1,1,n,bookings[i][0],bookings[i][1],bookings[i][2]);
        }
        vector<int> res;
        for(int i=1;i<=n;i++){
            res.push_back(query(1,1,n,i,i));
        }
        return res;
    }
};

有的没的

在考试中才学到的一些东西

昨天晚上考了《诗歌与哲学》这门课的结课考试，就两道题，都跟尼采有关。老师讲了一个学期的尼采，可惜我一个字没听，考到一半才意识到原来尼采不是古希腊的人。翻了半天书，看不太懂，但是看到了一段文字：

孤独者，有两种基本的性格类型：一是强者的孤独，一是弱者的孤独。前者源于个体的精神强大与体能强大，因这种强大和勇猛而傲视他人，保持个体的生存意志和生存原则，振奋自我的创造力，完成命定的事业；后者源于个体的精神强大与体能虚弱，对世界心怀仇恨与怨愤，与现实原则保持心灵的抗争，蔑视世俗者、伪信者和成功者。前者因内心与外力强大，虽孤独而勇于出击；后者因外力虚弱，虽自尊而怯于行动。孤独者善于吟唱孤独之歌，每个人在特殊的时刻，皆会有孤独的体验，但并非每个人皆能战胜孤独，迎接沸腾的生活。—— 李咏吟《文学批评学》

依然看不太懂，但是感受到了一丝触动和共鸣。也许是因为我也自诩蔑视世俗和伪信，立志做最真实的自己。人在夜来非的时候就是这么矫情吧。

环己三烯的冬眠舱

线段树（上）

概述